第一章绪论⚓︎

约 1497 个字 47 行代码预计阅读时间 8 分钟

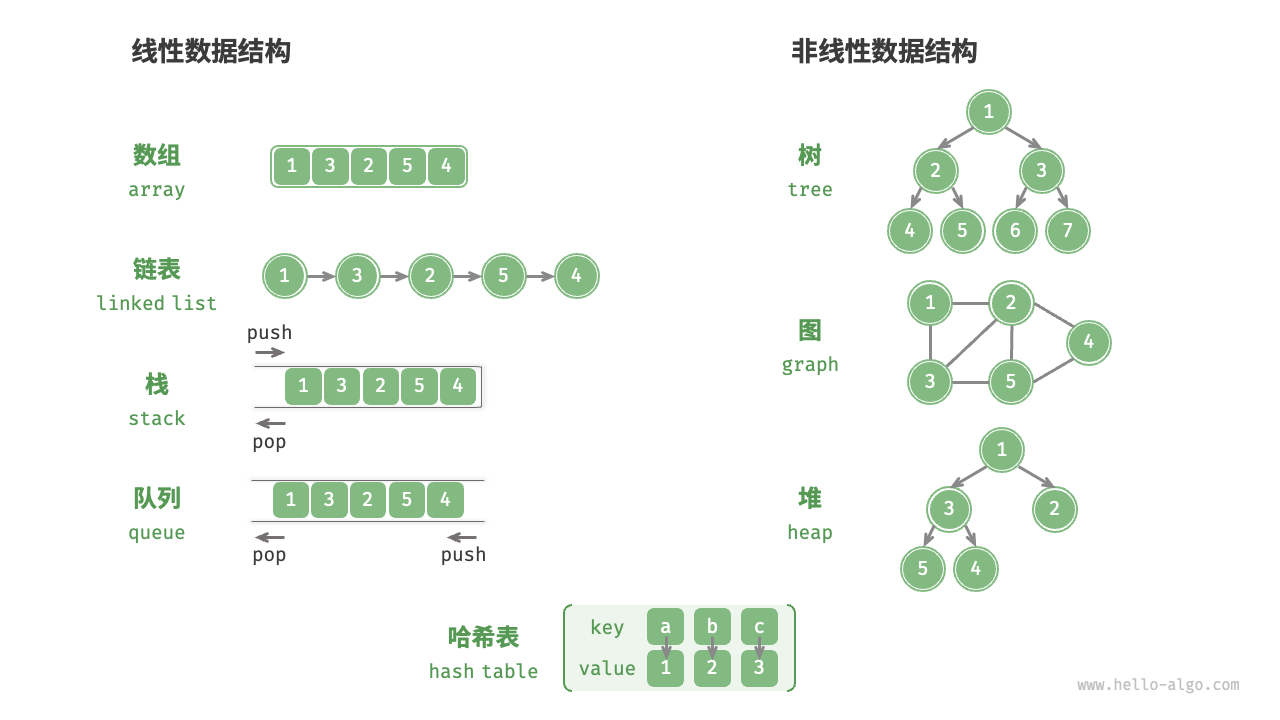
数据结构分类⚓︎

逻辑结构：线性与非线性

线性结构是一个数据元素的有序（次序）集

线性结构的特点

集合中必存在唯一的一个“第一元”

集合中必存在唯一的一个“最后元素 ”

除最后元素在外，均有唯一的后继

除第一元素之外，均有唯一的前驱

物理结构：连续与分散

1.1 数据结构讨论的范畴⚓︎

程序设计的核心：算法 + 数据结构 = 程序 (Algorithm + Data Structures = Programs)。这是由图灵奖得主尼古拉斯·沃斯提出的著名公式，指明了程序设计的两大基石。
- 数据结构：是问题的数学模型，研究如何组织数据。
- 算法：是处理问题的策略，研究如何操作数据。
程序设计问题的分类：
- 数值计算：如解线性代数方程组。
- 非数值计算：这是数据结构主要关注的领域，如信息管理系统（数据库）、计算机对弈、文本处理等。

1.2 基本概念⚓︎

一、数据与数据结构⚓︎

数据 (Data)：是能被计算机识别、存储和处理的符号的集合。
数据元素 (Data Element)：是数据的基本单位，在程序中通常作为一个整体进行考虑和处理。
数据项 (Data Item)：是组成数据元素的、有独立含义的最小单位。一个数据元素可以由若干个数据项组成。 > [注释]：可以这样理解：一个“学生”记录就是一个数据元素，而这个学生记录中的“姓名”、“学号”、“性别”等就是数据项。
数据结构 (Data Structure)：是相互之间存在一种或多种特定关系的数据元素的集合。
- 逻辑结构：指数据元素之间的逻辑关系，与数据的存储无关。它分为：
  1. 集合结构：元素之间除了“同属一个集合”外，没有其他关系。
  2. 线性结构：元素之间存在一对一的线性关系。
  3. 树形结构：元素之间存在一对多的层次关系。
  4. 图状结构：元素之间存在多对多的网状关系。
- 存储结构 (物理结构)：是数据的逻辑结构在计算机中的表示（或称映像）。主要有两种：
  1. 顺序存储：把逻辑上相邻的元素存储在物理位置也相邻的存储单元中。
  2. 链式存储：元素存储在任意的存储单元中，通过保存地址的指针来表示元素间的逻辑关系。

二、数据类型⚓︎

数据类型 (Data Type)：是一个值的集合和定义在这个集合上的一组操作的总称。
- 例如，C语言中的 int 类型，它的值是某个范围内的整数，操作包括加、减、乘、除等。

三、抽象数据类型 (ADT)⚓︎

定义 (Abstract Data Type)：指一个数学模型及定义在该模型上的一组操作。它强调的是“做什么”，而不是“怎么做”。
两大特征：
1. 数据抽象：描述实体时，只关注其本质特征和功能，忽略非本质细节。
2. 数据封装：将实体的内部实现细节隐藏起来，外部只能通过已定义的接口（操作）来访问。
描述方法：一个ADT通常用三元组 (D, S, P) 表示。
- D：数据对象。
- S：D上的关系集。
- P：对D的基本操作集。

ADT的表示与实现：在程序设计中，ADT需要通过语言中已有的固有数据类型（如struct、数组等）来实现。

例如，一个“复数”ADT，可以用C语言的struct来实现其存储，用函数来实现其加法等操作。

C
// 复数ADT的C语言实现示例

// 1. 存储结构定义
typedef struct {
    float realpart; // 实部
    float imagpart; // 虚部
} Complex;

// 2. 基本操作的函数原型声明
void AssignComplex(Complex *Z, float v1, float v2); // 构造复数
float GetReal(Complex Z); // 获取实部
float GetImag(Complex Z); // 获取虚部
void Add(Complex z1, Complex z2, Complex *sum); // 复数相加

// 3. 基本操作的函数实现
void Add(Complex z1, Complex z2, Complex *pSum) {
    // pSum 指向存储结果的变量
    pSum->realpart = z1.realpart + z2.realpart;
    pSum->imagpart = z1.imagpart + z2.imagpart;
}

1.3 算法和算法的量度⚓︎

一、算法 (Algorithm)⚓︎

定义：为了解决某类问题而规定的一个有限长的操作序列。
五个重要特性：
1. 有穷性：算法必须在执行有限步骤后终止。
2. 确定性：算法的每一步都有确切含义，无二义性。
3. 可行性：算法的每一步都必须是可行的，能通过有限次基本运算完成。
4. 输入：有零个或多个输入。
5. 输出：有一个或多个输出。

二、算法设计的原则⚓︎

正确性：算法应能正确地解决问题。
可读性：算法应易于人们阅读、理解和交流。
健壮性：当输入非法数据时，算法能适当地做出反应或进行处理，而不是产生异常或崩溃。
高效率与低存储量需求：即执行时间短（时间复杂度低），所需存储空间少（空间复杂度低）。

三、算法效率的衡量⚓︎

时间复杂度 (Time Complexity)：

目的：估算算法执行时间随问题规模n增大的变化趋势。
方法：通常不精确计算具体时间，而是计算算法中基本操作的重复执行次数，作为算法时间的衡量准则。
表示法：使用大O表示法，\(T(n) = O(f(n))\)。它表示随着问题规模n的增大，算法执行时间的增长率和\(f(n)\)的增长率相同。

示例1：矩阵乘法

C
void mult(int **a, int **b, int **c, int n) {
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            c[i][j] = 0;
            for (int k = 0; k < n; ++k) {
                // 基本操作是乘法和加法
                c[i][j] += a[i][k] * b[k][j];
            }
        }
    }
}

[分析]：最内层循环是基本操作，执行了 n*n*n 次。因此，时间复杂度为 \(O(n^3)\)。

示例2：选择排序

C
void select_sort(int a[], int n) {
    for (int i = 0; i < n - 1; ++i) {
        int j = i;
        // 这个内层循环是基本操作
        for (int k = i + 1; k < n; ++k) {
            if (a[k] < a[j]) {
                j = k;
            }
        }
        if (j != i) {
            int temp = a[j];
            a[j] = a[i];
            a[i] = temp;
        }
    }
}

[分析]：基本操作是比较。比较次数约为 \(n + (n-1) + ... + 1 = n(n-1)/2\)。因此，时间复杂度为 \(O(n^2)\)。

四、算法的存储空间需求⚓︎

空间复杂度 (Space Complexity)：
- 定义：算法在运行过程中占用的存储空间大小的度量，记作 \(S(n) = O(g(n))\)。
- 组成：算法本身占用的空间、输入/输出数据占用的空间、额外的辅助空间。
- 分析：通常我们只分析辅助空间。如果辅助空间相对于输入数据量来说是常数，则称此算法为原地工作。

第一章 绪论⚓︎