[toc]

一、基本概念

约 3661 个字 预计阅读时间 18 分钟

(一)误差

1. 误差的基本概念

测量的定义: 为确定被测对象的量值而进行的实验，是将被测量与一个作为测量单位的标准进行比较，获得比值的过程。

\(\text{被测量} \quad \text{标准量} \quad E \rightarrow q=\frac{L}{E} \quad \text{理想状态 } q=1 \text{}\)

• 标准量: 精度最高的标准量称为基准。是约定真值。
• \(q\) 反映被测量的数字: 反应被测量的数字包含数值、单位量纲和误差三个部分。

2. 误差的定义及表示法

• 误差 = 测得值 - 真值

真值: 观测一个量时，该量 本身 所具有的 真实 大小。

• 理论真值: 如三角形内角之和恒为 \(180^\circ\)。
• 约定真值/指定值/最佳估计值/约定值/参考值: 指对于给定用途具有适当不确定度的、赋予特定量的值。这个术语在计量学中常用。如国际千克基准 \(1 \text{kg}\)。约定真值 也具有一定的不确定度。

Note

误差是针对真值而言的，真值一般指约定真值。

• 误差的表示与性质

• 从表示形式上：误差可以分为 绝对误差、相对误差。

• 性质特点:

  ​ ① 系统误差: 准确性。

  ​ ② 随机误差: 精确性。

  ​ ③ 粗大误差。

Tip

下面分别讲述六种误差形式：绝对误差、相对误差、引用误差；最大绝对误差、最大相对误差、最大引用误差

（1）绝对误差 $$ 绝对误差 = 测得值 - 真值\ \Delta L = L - L_0 $$

• \(\Delta L\)：绝对误差；\(L\)：测得值；\(L_0\)：被测量的真值，常用约定真值代替。绝对误差就是一般所说的误差

  ① 绝对误差是一个具有确定的 大小、符号及单位 的量。

  ② 单位给出了被测量的量纲，其单位与测得值相同。

（2）修正值

• 定义: 为了消除固定的系统误差，用代数法而加到测量结果上的值。 $$ \text{真值} \approx \text{测得值} + \text{修正值} \ \text{修正值} \approx \text{真值} - \text{测得值} \approx -\text{误差},\ 测得值 = 真值+误差\ 测得值 = 真值-修正值、真值 = 测得值+修正值 $$

​ ① 与误差大小 近似相等，但方向相反。

​ ② 修正值本身还有误差。

• Example: 用某电压表测量电压，示值为 \(226\text{V}\) (测得值)，查检定证书，得知该电压表在 \(220\text{V}\) (真值) 附近的误差为 \(5\text{V}\) (绝对误差)，被测电压的修正值为 \(-5\text{V}\) (修正值)，则修正后的测量结果为 \(226 + (-5\text{V}) = 221\text{V}\) (测得值 + 修正值)。

（3）相对误差

• 定义: 绝对误差与 被测量真值 之比。 $$ r = \frac{\Delta L}{L_0} \text{} $$

• \(r\): 相对误差；\(\Delta L\): 绝对误差；\(L_0\): 真值。

  ① 相对误差有大小和符号。

  ② 无量纲，一般用百分数来表示。

  ③ 用相对误差可以 比较不同量值、不同单位、不同物理量 等的精确度。

（4）引用误差 <-- 相对误差

• 定义: $$ r_F = \frac{\Delta x}{x_m} $$

• \(r_F\): 引用误差；\(\Delta x\): 仪器某一刻度点的示值误差；\(x_m\): 该标称范围上限 (或量程) 。

• 引用误差是引用了特定值——标称范围上限（或量程）——得到的， 故该误差又称为 引用相对误差、满度误差。

（5）最大引用误差

• 定义: $$ r_m = \frac{\Delta x_m}{x_m} $$

• \(r_m\): 最大引用误差；\(\Delta x_m\): 仪器某标称范围 (或量程) 内的最大绝对误差；\(x_m\): 该标称范围 (或量程) 上限。

Warning

对于某一 仪器仪表 而言，最大引用误差具有 唯一性，其与实测值大小无关。用于表示仪器仪表的 精度等级，简单方便。

（6）电工仪表、压力表的准确度等级

当一个仪表的等级 \(s\) 选定后，用此表测量某一被测量时：

• 最大绝对误差为 (公式 1)

\[ \Delta x_m = \pm x_m \times s\% \text{} \]

• 最大相对误差为 (公式 2)

\[ r_x = \frac{\Delta x_m}{x} = \pm \frac{x_m}{x} \times s\% \text{} \]

​ ①: 绝对误差的最大值与该仪表的标称范围 (或量程) 上限 \(x_m\) 成正比。

​ ②: 选定仪表后，被测量的值越接近于标称范围 (或量程) 上限，测量的相对误差越小，测量越准确。对比最大引用误差的公式，知：在不超量程的情况下，最大引用误差是最大相对误差的最小值

Example.1 检定一只 \(2.5\) 级、量程为 \(100\text{V}\) 的电压表，发现在 \(50\text{V}\) 处误差最大，其值为 \(2\text{V}\)，而其他刻度处的误差均小于 \(2\text{V}\)，问这只电压表是否合格?

​ 解: 由公式 2，该电压表的最大引用误差为 $$ r_m = \displaystyle \frac{\Delta U_m}{U_m} = \frac{2}{100} = 2\% \text{} $$ 由于 \(2\% < 2.5\%\)，所以该电压表合格。

Example.2 某 \(1.0\) 级微安电流表，满度值 (标称范围上限) 为 \(100\)，求测量值分别为 \(100, 80\) 和 \(20\) 时的最大绝对误差和最大相对误差。

​ 解：根据题意，$s = 1.0, x_{m} = 100, x_1 = 100, x_2 = 80, x_3 = 20 $，有 ​ 最大绝对误差 \(\Delta x_m = \pm s \cdot x_m \% = \pm 1 uA\), ​ 最大相对误差分别为： ​ $r_{x_1} = \displaystyle \frac{\Delta x_m}{x_1} = \pm 1\% $ ​ $r_{x_2} = \displaystyle \frac{\Delta x_m}{x_2} = \pm 1.25\% $ ​ $r_{x_3} = \displaystyle \frac{\Delta x_m}{x_3} = \pm 5\% $

Important

含义	表达式
绝对误差	\(\Delta L = L - L_0\), \(\Delta x\)
相对误差	\(r = \displaystyle \frac{\Delta L}{L_0}\)
引用误差	\(r_F = \displaystyle \frac{\Delta x}{x_m}\)
最大引用误差	\(r_m= \displaystyle \frac{\Delta x_m}{x_m}\)
最大绝对误差	$\Delta x_m = \pm s \cdot x_m \% $
最大相对误差	\(r_x = \displaystyle \frac{\Delta x_m}{x}\)

3. 误差的来源

• 误差来源分类:

• (1) 测量装置误差: 零部件配合的不稳定性、变形、表面油膜不均匀、摩擦等。仪器机构设计原理上的缺点，零件制造和安装不正确，附件制造偏差。

• (2) 测量环境误差: 指各种环境因素与要求条件不一致而造成的误差。

• (3) 测量方法误差 (理论误差): 指使用的测量方法不完善，或采用近似的计算公式等原因所引起的误差。

• (4) 测量人员误差: 测量人员的工作责任心、技术熟练程度、生理感官与心理因素、测量习惯等的不同而引起的误差。

---

4. 误差分类

Caution

这一章节有一个常用到的概念 ① “[对同一被测量] [进行无限多次测量] [所得结果的平均值]”

• 系统误差
• 随机误差
• 粗大误差

（1）系统误差

a.定义: 在重复性条件下，对同一被测量进行无限多次测量所得结果的平均值 与被测量的真值之差。

b.特征: 在相同条件下，多次测量同一量值时，该误差的绝对值和符号 保持不变，或者在条件改变时，按某一 确定规律变化 的误差。

Example:

① 用天平计量物体质量时，砝码的质量偏差。

② 用千分表读数时，表盘安装偏心引起的示值误差。

③ 刻线尺的温度变化引起的示值误差。

c. 分类:

**① 按对误差掌握程度**
  1）**已定系统误差**: 误差绝对值和符号已经明确的系统误差。
  2）**未定系统误差**: 误差绝对值和符号未能确定的系统误差，但通常估计出误差范围。

**② 按误差出现规律**
  1）**不变系统误差 (恒定系统误差)**: 误差绝对值和符号固定不变的系统误差。
  2）**变化系统误差 (可变系统误差)**: 误差绝对值和符号变化的系统误差。按其变化规律，可分为线性系统误差、周期性系统误差和复杂规律系统误差。

（2）随机误差

a. 定义: 测得值与 在重复性条件下对同一被测量进行无限多次测量结果的平均值 之差。又称为 偶然误差。

b. 特征: 在相同测量条件下，多次测量同一量值时，绝对值和符号以 不可预定方式变化 的误差。

c. 产生原因: 实验条件的 偶然性微小变化，如温度波动、噪声干扰、电磁场微变、电源电压的随机起伏、地面振动等。

d. 性质: 随机误差的大小、方向均 随机不定，不可预见，不可修正。经过大量的重复测量可以发现，它是 遵循某种统计规律 的，可以用概率统计的方法处理。

随机误差分布图

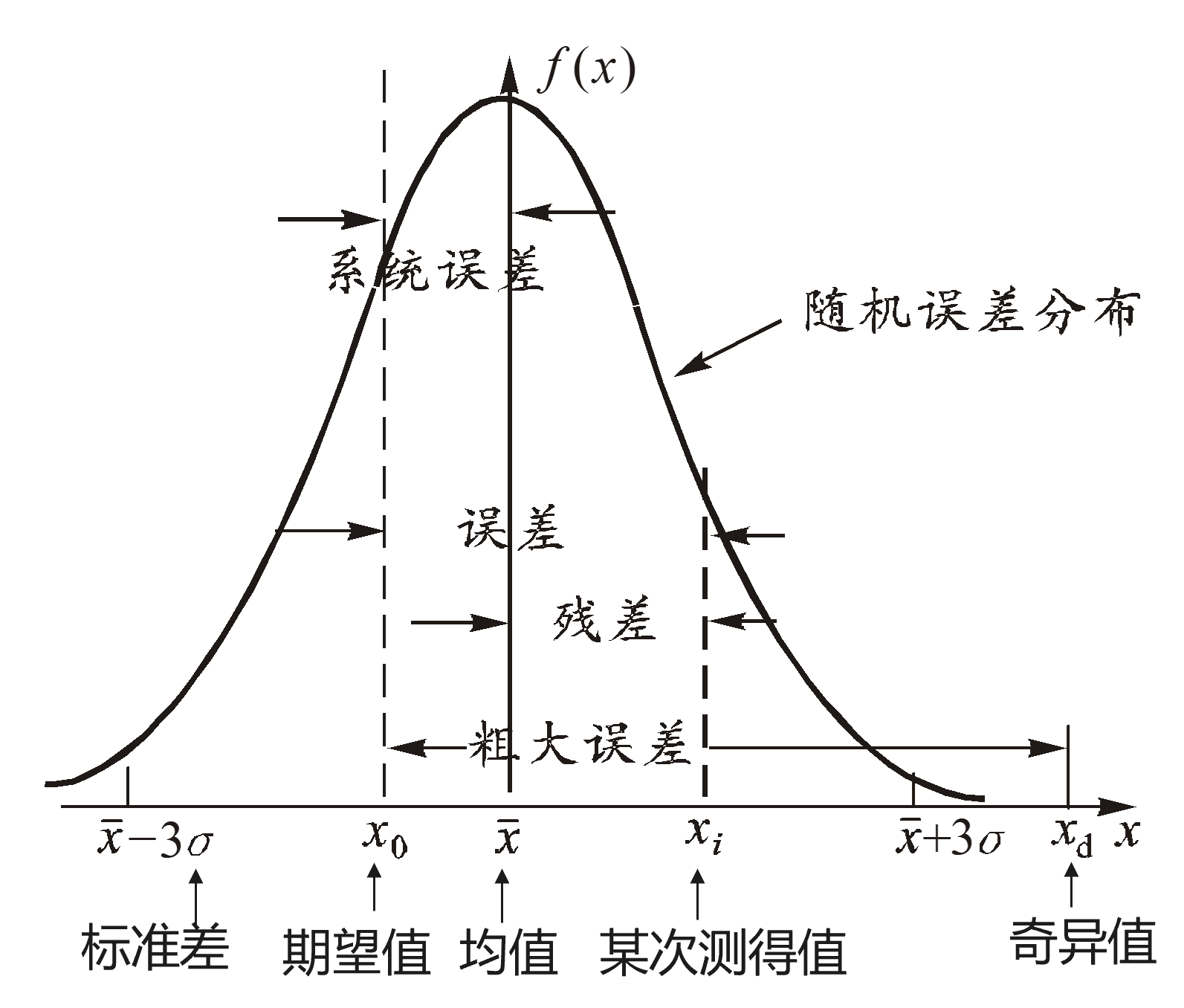
（3）粗大误差

a. 定义: 指 明显超出统计规律预期值 的误差。又称为 疏忽误差、过失误差 或简称 粗差。

b. 产生原因: ① 测量方法不当或错误，测量操作疏忽和失误 (如未按规程操作、读错读数或单位、记录或计算错误等)。 ② 测量条件的突然变化 (如电源电压突然增高或降低、雷电干扰、机械冲击和振动等)。

---

(二)精度

• 准确度: 只考虑 系统误差 的大小时，准确度称为准确度。

• 精密度: 只考虑 随机误差 的大小时，准确度称为精密度。

• 精确度: 表示测量结果与被测量真值之间的 一致程度。就误差分析而言，精确度是测量结果中 系统误差和随机误差的综合。误差大，则精确度低；误差小，则精确度高。

Warning

精确度 (精度) 在数值上一般多用 相对误差 来表示，但不用百分数。如某一测量结果的相对误差为 \(0.001\%\)，则其精度为 \(10^{-5}\)。

（1）准确度、精密度和精确度三者之间的关系

情况	弹着点分布描述	误差特点	精度结论
(a)	弹着点全部在靶上，但分散	系统误差小，随机误差大	精密度低，准确度高
(b)	弹着点集中，但偏向一方	系统误差大，随机误差小	精密度高，准确度低
(c)	弹着点集中靶心，命中率高	系统误差与随机误差均小	精密度、准确度都高，从而精确度亦高

（2）常用名词术语

• a. 重复性: 指在 相同条件下在短时间内 对同一个量进行多次测量所得测量结果之间的一致程度。一般用测量结果的分散性来定量表示。
• b. 复现性 (再现性): 指在 变化条件下，对同一个量进行多次测量所得测量结果之间的一致程度。一般用测量结果的分散性来定量表示。
• c. 稳定性: 指测量仪器保持其计量特性随时间恒定的能力。可以用计量特性变化某个规定的量所经过的时间；或用计量特性经规定的时间所发生的变化等来定量表示。
• d. 示值误差: 指测量仪器的示值与对应输入量的真值之差。实际应用中常采用约定真值。
• e. 偏移: 指测量仪器示值的 系统误差。通常用适当次数重复测量的示值误差的平均来估计。
• f. 最大允许误差 (允许误差限): 指对于给定的测量仪器，规范、规程等所允许的误差极限值。
• e. 不确定度: 与测量结果相关联的、用于合理表征被测量值 分散性大小 的参数。它是定量评定测量结果的一个重要质量指标。

---

(三)有效数字

（1）有效数字

• 定义: 含有误差的任何数 ，如果其绝对误差界是最末尾数的半个单位，那么从这个近似数左方起的第一个非零的数字，称为第一位有效数字。从第一位有效数字起到最末一位数字止的所有数字，不管是零或非零的数字，都叫有效数字。

Note

实际测量的数字除 最后一位是可疑 的，其余的数字都是确定的。

​ Example:

​ ① 对于小数，第一个非零有效数字前面的零不是有效数字。如: \(0.0023\) 有效数字为最后 \(2\) 位。

​ ② 数据末尾的一个或数个零应为有效数字。如 \(1450\) 有效数字应为 \(4\) 位， \(0.460\) 有效数字为 \(3\) 位。

​ ③ 数字末尾的零的含义有时并不清楚，此时往往采用 \(10\) 的方次表示。如 \(12000 \text{m}\) 表示为 \(1.2 \times 10^4\)，有效数字为 \(2\) 位，若写成 \(1.20 \times 10^4\)，有效数字为 \(3\) 位。

• 测量结果保留原则:

​ ① 最末一位数字是 不可靠 的，而倒数第二位数字是 可靠 的。 ​ ② 在进行重要的测量时，测量结果和测量误差可比上述原则 再多取一位数字 作为参考。

（2）数字舍入规则：四舍六入五留双

​ ① （6入）若舍去部分的数值，大于 保留部分末位的半个单位，则末位数 加 1。

​ ② （4舍）若舍去部分的数值，小于 保留部分末位的半个单位，则末位数 不变 (此处原文似有误，应为“末位数不变”)。

​ ③ （5留双）若舍去部分的数值，等于 保留部分末位的半个单位，则末位 凑成偶数，即当末位为偶数时则末位不变，当末位是奇数时则末位加 1。

​ Example.1:

• (1) 将 \(3.14159\) 分别取 \(3\)、\(4\) 位有效数字?

​ 答: 根据规则一、规则二，舍入后的有效数字分别为 \(3.14\) 和 \(3.142\)。

• (2) \(2.55\) (保留二位有效数字) 为 \(2.6\)

• (3) \(2.64\) (保留二位有效数字) 为 \(2.6\)

（3）数字运算规则

① （过程）近似数运算时，为保证最后结果有尽可能高的精度，所有残余 运算 的数字，在有效数字后 可多保留一位数字 作为参考数字(或称为安全数字)。

② （加减）近似数做加减运算，运算数据以 小数位数最少 的数据位数 为准，其余数据 可多取一位小数，但最后结果应与小数位数最少的数据小数位相同。

③ （乘除）近似数做乘除运算，运算数据以 有效位数最少 的数据位数 为准，其余数据 可多取一位有效数，但最后结果应与有效位数最少的数据位数相同。

④ （幂次）在近似数平方或开方运算时，近似数的选取与乘除运算相同。

⑤ （对数）在对数运算时，n 位有效数字的数据应该用 n 位对数表，或用（n+1） 位对数表，以免损失精度。

⑥ （三角）三角函数运算时，所取函数值的位数应随角度误差的减小而增多， 其对应关系：

角度误差	10‘	1'	0.1'	0.01'
函数值位数	5	6	7	8

Tip

1. 精度的确定 加减看小数位数最少的数据，保留到该小数位 乘除看有效数字位数最少的数据，保留到该小数位 其他规则见上
2. 运算过程的精度 可多取一位运算，及运算时的精度为，目标精度/目标精度多一位

• (1) \(2643.0 + 987.7 + 4.187 + 0.2354\)

  ​ \(2643.0 + 987.7 + 4.19 + 0.24\) (加减法按照小数点保留，但是计算过程中比基准精确度多取一位)

  ​ \(= 3635.13\)

  ​ \(\approx 3635.1\) (加减法按照小数点保留)

• (2) \(15.13 \times 4.12 = 62.3356 \approx 62.3\) (乘法按照有效数字保留)

---